In electrochemical energy storage devices, both electronic conduction and ion diffusion play a crucial role in determining the performance of electrode materials. Taking lithium-ion batteries as an example (Figure 1), electrons are transported to the surface of the material through the external circuit, while ions diffuse through the internal circuit, ultimately leading to electrochemical reactions among the active material, electrons, and ions, enabling the conversion between electrical and chemical energy. Generally, the electron transfer in the external circuit is faster than ion diffusion in the internal circuit. Therefore, continuous improvement of the material interface properties is necessary to achieve rapid charge balance, avoid net charge accumulation on the material surface, and reduce polarization during fast charge-discharge processes [1]. In summary, ion diffusion within the material is a critical reaction process and a limiting step in electrochemical reactions. Accurate characterization of ion diffusion is of paramount importance for guiding the design and synthesis of electrode materials.
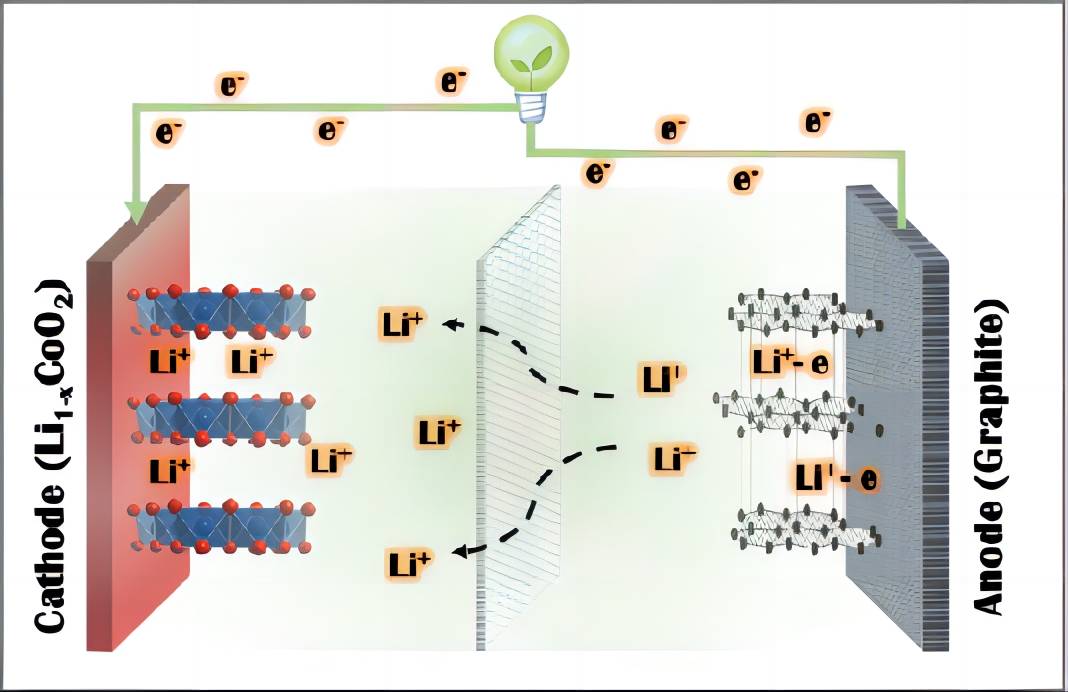
Figure 1 Conduction behavior of electrons and ions in a lithium-ion battery
Ion diffusion within the material refers to the phenomenon of ion transport from regions of high concentration to regions of low concentration, resulting in homogenization of ion concentration within the material [1]. The physical parameter that characterizes the rate of ion diffusion is the ion diffusion coefficient. Common testing methods for determining the ion diffusion coefficient include Galvanostatic Intermittent Titration Technique (GITT), Potentiostatic Intermittent Titration Technique (PITT), Cyclic Voltammetry (CV), Electrochemical Impedance Spectroscopy (EIS), Current Pulse Relaxation (CPR), Potentiostatic Current Step Amperometry (PSCA), and Potentiostatic Relaxation Technique (PRT). This article focuses on GITT technology and provides a detailed summary of its testing principles, methods, and application examples.
Galvanostatic Intermittent Titration Technique (GITT) is a testing technique that analyzes the relationship between potential and time to obtain information about reaction kinetics. It was initially proposed by German scientist W. Weppner. A complete GITT test consists of multiple "current step" units, as shown in Figure 2. Within each current step unit (Figure 3), the electrochemical system is subjected to transverse charging and discharging at a low current for a certain period. Then, the applied current is interrupted, and a certain period is maintained to allow ions to fully diffuse within the active material and reach an equilibrium state. By analyzing the changes in electrode potential and relaxation time and combining them with physicochemical parameters of the active material, the diffusion coefficient of ions within the material can be inferred and calculated.
Since the GITT test assumes that ion diffusion mainly occurs in the surface layer of the solid-phase material, the following constraints are applied to the applied current time (t1) and relaxation time (t2):
a) The application time of the current pulse (t1) must be sufficiently short, at least satisfying t1 << L²/D, where L is the characteristic length of the material and D is the diffusion coefficient of ions.
b) The relaxation time (t2) must be long enough to ensure that Li+ ions diffuse sufficiently within the active material to reach an equilibrium state, with a stable voltage as the criterion.
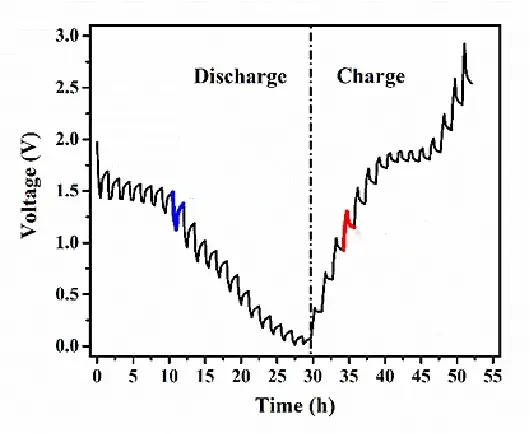
Figure 2 complete GITT curve
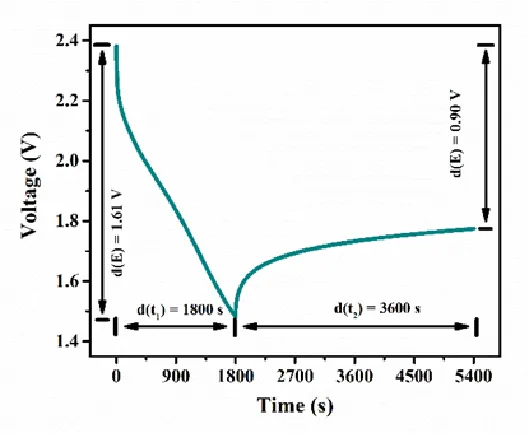
Figure 3 curve of voltage and time in a current step
The theoretical basis for determining the ion diffusion coefficient in GITT is derived from Fick's laws. Since Fick's first law applies only to steady-state diffusion, where the concentration of diffusing species varies only with distance and not with time, it cannot fully describe the diffusion of lithium ions in materials, which involves both steady-state and non-steady-state behaviors. Therefore, Fick's second law, which describes the variation of diffusing species' concentration with both distance and time, is used.
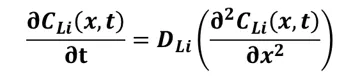
By incorporating initial conditions, boundary conditions, and neglecting volume changes within active material particles, Fick's second law can be solved to obtain the diffusion coefficient D:
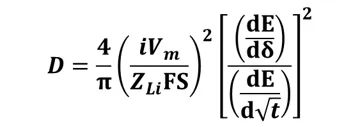
where the known parameters are i (current in mA), Z_(Li-) (charge number of lithium ions, 1), F (Faraday's constant, 96485 C/mol), S (electrode/electrolyte contact area), and the unknown parameters are dE/dδ (slope of the Coulomb titration curve) and dE/d√t (relationship between potential and time) [2].
When the applied current is sufficiently small, and the relaxation time (τ) is short enough, the relationship between dE/d√t becomes linear, simplifying the calculation formula further:
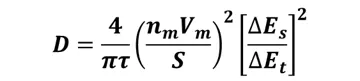
In which: τ is the relaxation time, n_(m) is the number of moles, V_(m) is the molar volume, S is the electrode/electrolyte contact area, ∆E_(s) is the total voltage change caused by the pulse, and ∆E_(t) is the voltage change during constant current charge/discharge.
It is worth noting that at the moment when the electrode is subjected to current, due to the presence of ohmic resistance and charge transfer impedance, the electrode potential rapidly increases/decreases. This entire process is transient behavior. Subsequently, when the current is maintained constant, the potential starts to change slowly. Therefore, the ∆Et during charge/discharge does not include the voltage change caused by iR, as shown in Figure 4. Additionally, it can be observed that the magnitude of D is related to the relaxation time. Hence, to ensure accurate test results, a sufficiently long relaxation time should be chosen to ensure that the electrode potential remains essentially unchanged.
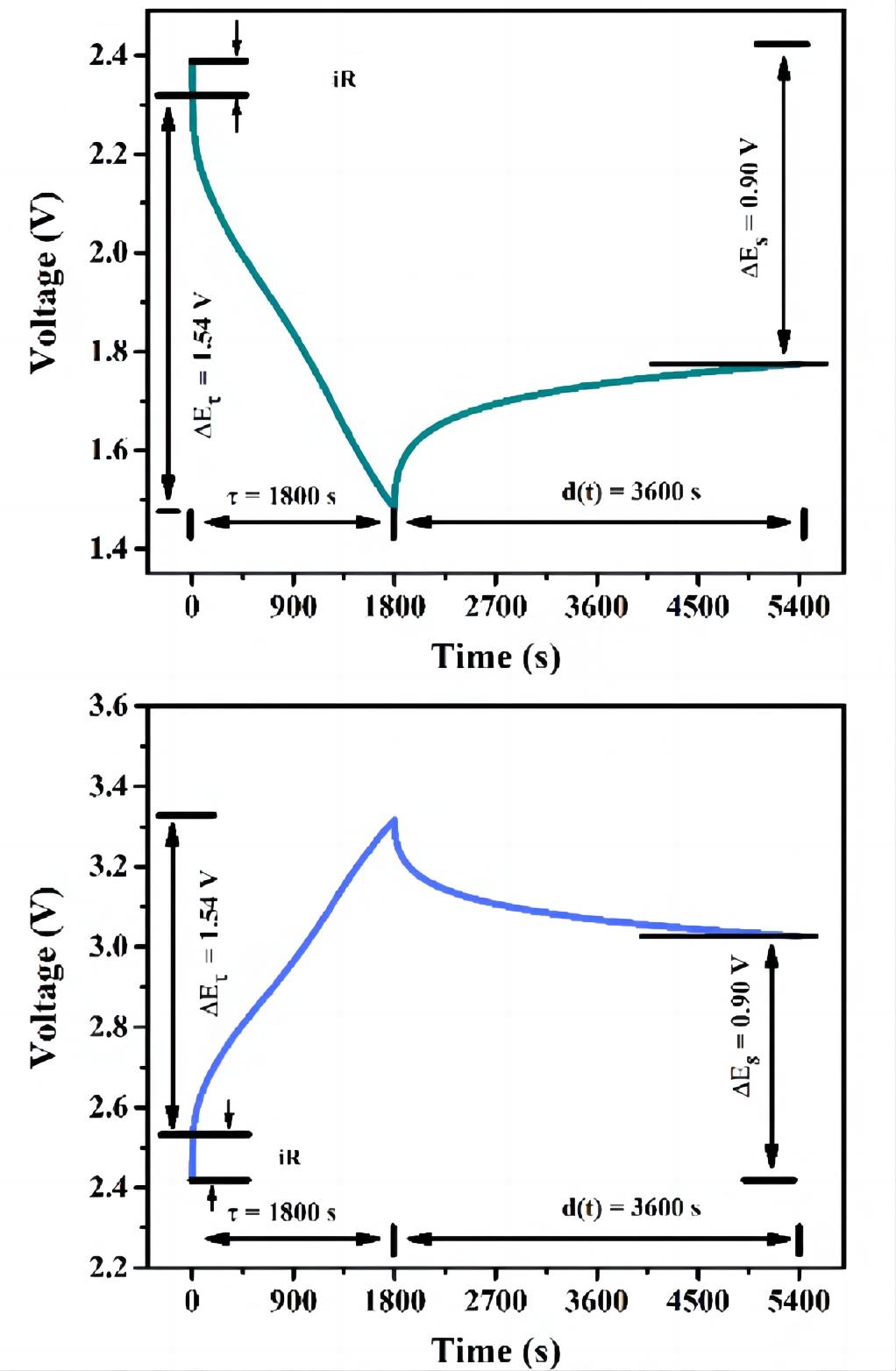
Figure 4 current step during discharge (top)/charge (bottom) in GITT curve
By obtaining the ∆Es and ∆Et for each "pulse-relaxation" unit, it is possible to calculate the variation of lithium ion diffusion rate with potential/charge-discharge depth throughout the entire charge-discharge process, as shown in Figure 5.
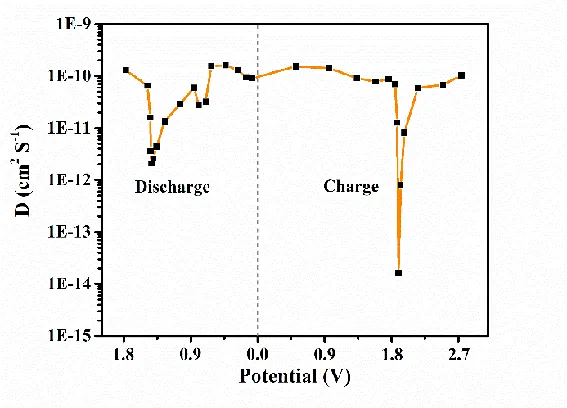
Figure 5 diffusion coefficient of lithium ion at different potential
GITT is generally performed using charge-discharge testers or electrochemical workstations. Taking the NEWARE constant current charge-discharge tester as an example, the GITT testing process is described.
(1) Double-click the NEWARE constant current charge-discharge tester software (Figure 6) to enter the testing interface (Figure 7).
Figure 6 NEWARE battery tester software-BTS8.0.0

Figure 7 NEWARE constant current charge discharge tester main interface
(2) Select a testing channel and right-click to enter the step editing interface. The testing procedure can refer to the provided step testing template. The pulse constant current used in GITT testing is generally small, and a calculation of 0.1C/0.1A can be selected. The pulse time should be relatively short, typically between 10-30 minutes. The diffusion time (relaxation time) should be sufficiently long, ensuring that the voltage recovers to a state where it essentially no longer changes. Please note that the parameter values shown in the figure are for demonstration purposes only. The specific parameter values should be determined based on the requirements of the experiment.
 Figure 8 GITT test procedure for setting up typical anode materials
Figure 8 GITT test procedure for setting up typical anode materials
(3)The data after the test is shown in the figure 9
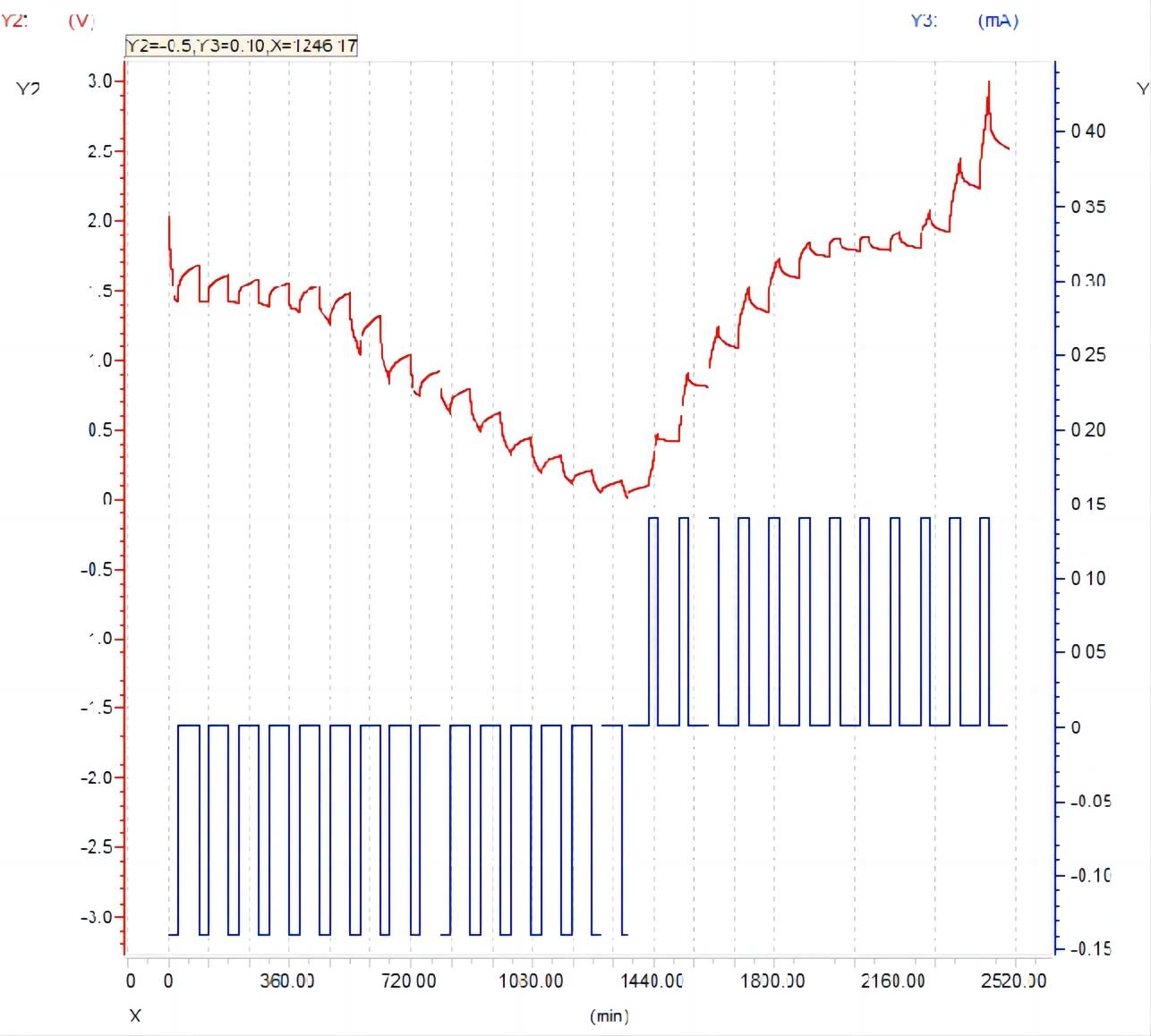
Figure 9 data display after GITT test
For GITT testing, whether to discharge first or charge first should be consistent with constant current charge-discharge testing. For example, when S, V₂O₅, and FePO₄ positive electrode materials are paired with Li, it is necessary to discharge first before charging. Therefore, in GITT testing, discharge should be performed before charging.
Example 1: The authors reported a novel high-temperature and high-loading phosphate iron lithium (UCFR-LFP) composite electrode. The cycling and rate capability tests showed that this electrode outperformed the traditional phosphate iron lithium electrode (Con-LFP) in both rate performance and cycling stability. Through GITT testing, it was found that the average lithium ion diffusion coefficient of the UCFR-LFP electrode (3.6×10⁻¹¹ cm² s⁻¹) was significantly higher than that of Con-LFP (5×10⁻¹² cm² s⁻¹). Combined with other structural characterizations, the authors analyzed that this could be attributed to the unique composite porous structure of UCFR-LFP, which ensures close contact between the active material and the conductive agent, promotes electrolyte diffusion and transport throughout the electrode, and optimizes the electron and ion transport pathways of the electrode.
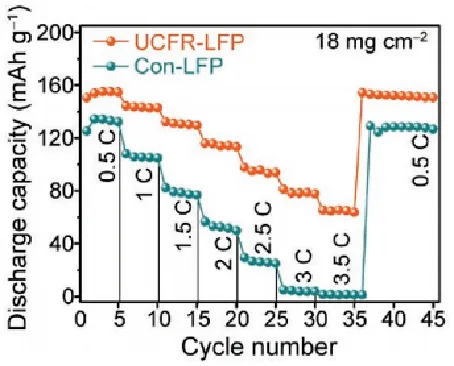
Figure 10 comparison of magnification performance of two LFP electrodes[2]
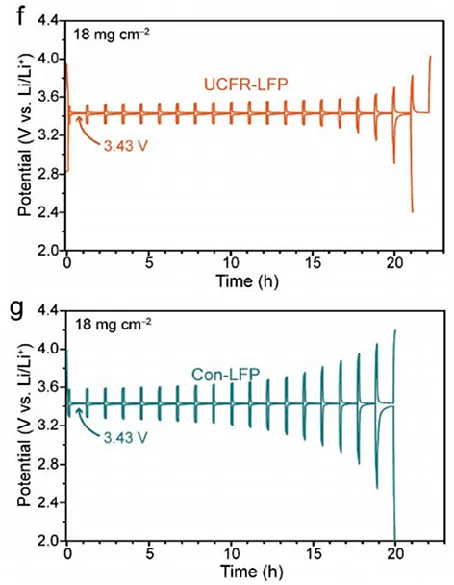
Figure 11 comparison of GITT curves of two LFP electrodes[3]
Example 2: The authors reported a series of potassium vanadate nanomaterials as positive electrode materials for aqueous zinc-ion batteries (ZIBs). Through GITT analysis, it was found that potassium vanadates with tunnel structures, such as K₂V₈O₂₁ and K_(0.25)V₂O₅, facilitated zinc ion diffusion, while layered KV₃O₈ and K₂V₆O₁₆·1.57H₂O, which are prone to structural collapse, exhibited low zinc ion diffusion coefficients, making it difficult to achieve high capacity.
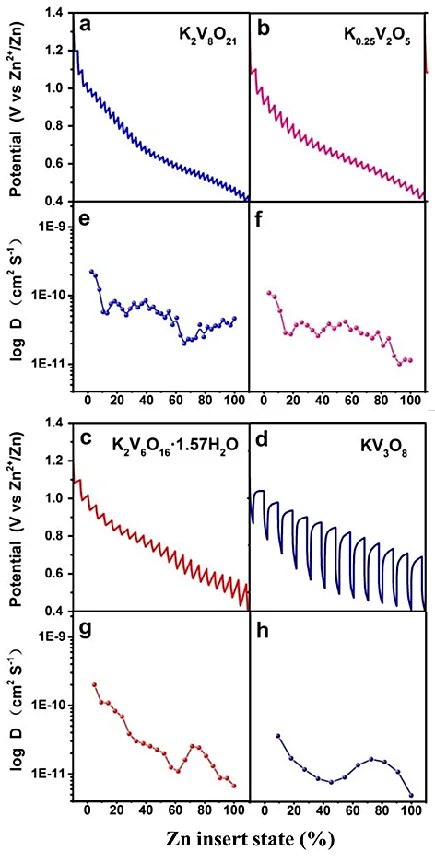
Figure 12 GITT curves for four electrodes (a-d) and zinc ion diffusion coefficients (e-h)[4]
[1].ZHENG Hao, GAO Jian, WANG Shaofei, LI Hong. Fundamental scientific aspects of lithium batteries (VI)--Ionic transport in solids[J]. Energy Storage Science and Technology, 2013, 2(6): 620-635.
[2].LING Shigang, WU Jiaoyang, ZHANG Shu, GAO Jian, WANG Shaofei, LI Hong. Fundamental scientific aspects of lithium ion batteries(ⅫⅠ) —Electrochemical measurement[J]. Energy Storage Science and Technology, 2015, 4(1): 83-103.
[3].Li H, Peng L, Wu D, et al. Ultrahigh-Capacity and Fire-Resistant LiFePO4-Based Composite Cathodes for Advanced Lithium-Ion Batteries[J]. Advanced Energy Materials, 2019, 9(10):1802930.
[4]. Boya T, Guozhao F, Jiang Z, et al. Potassium vanadates with stable structure and fast ion diffusion channel as cathode for rechargeable aqueous zinc-ion batteries[J]. Nano Energy, 2018, 51: 579-587.
NEWARE TECHNOLOGY LLC
755 Ames Avenue, Milpitas, CA, USA, 95035










